Top 6 Types of Experimental Designs | Statistics

The following points highlight the top six types of experimental designs. The types are: 1. Completely Randomized Design 2. Randomized Block Design 3. Latin Square Design 4. Split Plot Design 5. Lattice Design 6. Augmented Designs.

Experimental Design: Type # 1. Completely Randomized Design (CRD):

The design which is used when the experimental material is limited and homogeneous is known as completely randomized design. This design is specially used for pot culture experiments.

The important characteristics of this design are given below:

i. Layout:

The whole field is divided into plots of similar shape and size. The number of plots is equal to the product of treatments and replications. These plots are then serially numbered.

ii. Replications:

There is no restriction on the number of replications in this design. The number of replications can vary from treatment to treatment. Normally, the number of replications for different treatments should be equal to get the estimates of treatment effects with same precision. The number of replication depends on the availability of experimental material and level of precision required.

If the experimental material for some treatments is available in limited quantities, the number of replications in such case can be reduced. If the estimates of certain treatments effects are required with more precision, the number of their replications is increased. This type of flexibility in the choice of replications is present in this design only.

iii. Randomization:

The randomization is done treatment wise with the help of random table. First random numbers equal to the number of plots are taken from the random table. From these random numbers each treatment is assigned numbers as per number of replications. Then random numbers of each treatment are allotted to the plots bearing the serial number similar to the random number.

iv. Local Control:

The principle of local control or error control is not adopted in this design. The error variance can only be reduced by selecting a homogeneous set of experimental units. This is possible when the experimental area is limited. When the number of treatments is large, it may not always be possible to get a large homogeneous set of experimental units. Under such situations, it is hot desirable to adopt CRD.

v. Variation:

In this design, the total variation is split into two components, namely variation due to treatments and variation due to error.

vi. Standard Error:

The standard error is calculated as, where, VE = pooled error variance and r₁ and r₂ are number of replications. If r₁ = r₂ the formula is reduced to .

Merits:

i. Layout:

The layout of this design is simple. In this design, any number of treatments and replications can be used.

ii. Analysis:

The analysis of this design is simple. The analysis remains simple even when some of the observations are missing or rejected.

iii. Accuracy:

This design provides maximum number of degrees of freedom for the estimation of error as compared with other designs for a given number of treatments and experimental units.

Demerits:

i. There is a basic assumption about the homogeneity of plots or experimental units which is rarely met in field experiments. Hence this design is not suitable for field experiments.

ii. This design is not suitable when there is fertility variation in the field because no local control is provided in this design.

Uses:

i. This design is useful for pot culture experiments where it is possible to obtain homogeneous material.

ii. This design is recommended when some of the experimental units will fail to respond or likely to be destroyed.

Assuming 5 treatments and 4 replications the analysis of variance table for CRD is given below (Table 36.3).

Experimental Design: Type # 2. Randomized Block Design (RBD):

The experimental design which controls the fertility variation in one direction only is known as randomized block design (RBD). Adoption of this design is useful when the variation between the blocks is significant.

The main features of this design are briefly presented below:

i. Layout:

First the experimental field is divided into homogeneous groups equal to the number of replications. These homogeneous groups are known as blocks. Then each block is further divided into plots of similar shape and size equal to the number of treatments.

ii. Replications:

There is no restriction on the number of replications. However, all the treatments should have equal number of replications.

iii. Randomization:

The treatments are allotted to the plots in each block by a random process. Separate randomization is used in each block.

iv. Local Control:

The principle of local control or error control is adopted in this design by forming homogeneous blocks.

v. Variation:

In this design, the total variation is split into three components, namely blocks, treatments and error (Table 36.4).

vi. Standard Error:

The standard error is calculated as . If some treatments have extra replications, the SE will be calculated as .Where, r₁ and r₂ are the number of replications of the treatment to be compared.

Merits:

i. Layout:

The layout and analysis of this design are very simple. The data can be analysed even when observations of some plots are missing on account of damage caused by animals, insects or flood. In such case one or two damaged replications can be discarded and analysis can be performed with the data of remaining replications.

ii. Efficiency:

A large number of treatments can be tested by this design, but the efficiency of error control decreases beyond 20 due to increase in heterogeneity within the block.

iii. Accuracy:

This design provides more accurate results than CRD due to formation of homogeneous blocks. This design controls the fertility variation in one direction.

Demerits:

i. When the missing values are numerous, this design is less convenient than CRD because the analysis becomes more complicated.

ii. The efficiency of error control decreases when the number of treatments becomes more than 20, because increase in treatment increases the heterogeneity within the block.

Uses:

This design can be used when the fertility variation moves in one direction. In this design error is reduced by forming homogeneous blocks.

Assuming 5 replications and 10 varieties, the analysis of variance for RBD is given below:

Experimental Design: Type # 3. Latin Square Design (LSD):

The experimental design which simultaneously controls the fertility variation in two directions is called Latin square design (LSD). In other words, Latin square designs are adopted for eliminating the variation of two factors which are generally called rows and columns.

The main features of Latin square design are briefly described below:

i. Layout:

In this design the field is divided into homogeneous blocks in two ways. The blocks in one direction are commonly known as rows and the blocks in other direction as columns. The number of plots in each row is the same as the number of plots in each column. This number is equal to the number of treatments.

ii. Replications:

In this design, the number of replications per treatment is always equal to the number of treatments.

iii. Randomization:

The treatments are assigned in such a way that every treatment occurs once and only once in each row and each column. The easiest way of obtaining such randomization is to start with reduced Latin square, which is the one in which the first row and first column are arranged in alphabetical order, and then reshuffling the rows, columns and treatments with the help of random numbers.

iv. Local Control:

The principle of local control is adopted in this design. This design controls the experimental error by forming rows and columns.

v. Variation:

In this design, the total variation is separated into four components, namely rows, columns, treatments and error (Table 36.5).

vi. Standard Error:

The standard error is calculated as , where VE = error variance and n = number of replications.

Merits:

i. Layout and Analysis:

The layout and analysis of this design are simple.

ii. Accuracy:

This design provides more accurate results than CRD and RBD because the fertility variation is controlled in two directions.

iii. Efficiency:

This design is useful for comparing a small group of treatments. The maximum number of treatments for which we can use Latin square design is 12.

iv. When data from some of the plots are missing, Yates’ missing plot technique can be used for analysis of data.

Demerits:

i. This design is less flexible and does not permit any number of replications for any treatment. The number of replications is always equal to the number of treatments.

ii. This design can be used only for small number of treatments (maximum 12) because the number of experimental units required for this design increases rapidly with the increase in the number of treatments.

iii. In the field experiments, it is easier to manage RBD than LSD because RBD can be used even when the field is in strips or rectangular, while LSD requires square shaped field.

Uses:

This design is used when fertility moves in two directions.

Experimental Design: Type # 4. Split Plot Design (SPD):

The experimental design in which experimental plots are split or divided into main plots, sub­plots and ultimate-plots is called split plot design (SPD). In this design several factors are studied simultaneously with different levels of precision. The factors are such that some of them require larger plots like irrigation, depth of ploughing and sowing dates, and others require smaller plots.

The important characteristics of SPD are briefly described below:

i. Layout:

The layout of this design consists of four steps as given below:

(a) First the experimental field is divided into homogeneous blocks equal to the number of replications

(b) Then each block is divided into a number of plots equal to the number of levels of the first factor. These plots are known as main plots.

(c) Then each main plot is divided into a number of sub-plots equal to the number of levels of second factor.

(d) Then each sub-plot is divided into a number of ultimate plots equal to the number of levels of third factor.

ii. Replications:

There is no restriction on the number of replications unlike LSD. However, the number of replications should be uniform for all the treatments.

iii. Randomization:

The levels of the first factor are applied to the main plots of each block by the random process. The sub-plot treatments are then allotted at random to the sub-plots within each main plot. A separate randomization is carried out for each main plot. The levels of third factor are allotted to the ultimate plots in each sub-plot by a separate randomization.

iv. Local Control:

The principle of local control is adopted in this design by forming homogeneous blocks.

v. Variation:

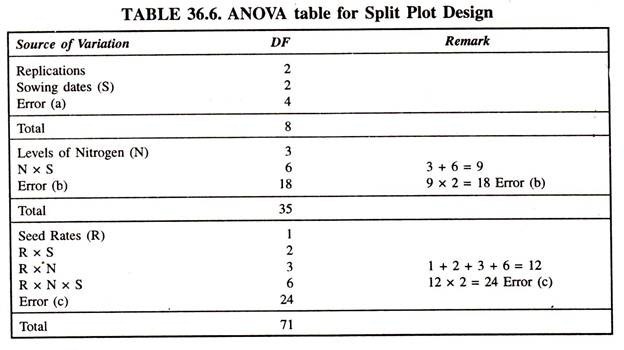
In this design, the total variation is divided into several components, i.e., blocks, first factor, second factor, third factor, their combinations and error a, b and c (Table 36.6).

Merits:

i. Accuracy:

The effects of main plot, sub-plot and ultimate plots are estimated with increasing trends of precision, while in RBD main effects and interactions are estimated with the same precision.

ii. Efficiency:

Several factors out of which some require larger plots and others smaller plots can be tested in a single experiment with a very little extra cost.

iii. By inclusion of more factors in a experiment we can get additional information without spending much for the same.

Demerits:

i. The layout and analysis of this design are more complicated as compared to that of RBD and LSD.

ii. This design provides lesser degrees of freedom for the estimation of error variance than RBD.

Uses:

i. This design is useful when all the factors are not of equal importance, i.e., some of them require larger plots and others require smaller plots.

ii. When some of the factors have small amount of material, they can be used as sub-plots or ultimate plots in this design.

The analysis of variance for SPD assuming 3 replications, 3 main plots (sowing dates), 4 sub­plots (4 N levels), and two ultimate plots (seed rates) is given below:

Experimental Design: Type # 5. Lattice Design:

Lattice designs are incomplete block designs in which the number of varieties or treatments forms a square.

The important characteristics of lattice design are given below:

i. Layout:

The experimental field is divided into homogeneous parts equal to the number of replications. Each part is further divided into plots of equal size in such a way that the number of plots should form a square and each replication has equal plots in each direction (i.e., equal rows and columns).

ii. Replications:

There is no restriction on the number of replications. It would be better if the number replication is 4 because it would make the layout compact.

iii. Randomization:

The treatments are randomized replication wise. Separate randomization is done in each replication.

iv. Variation:

The total variation is divided into five components, namely replications, rows, columns, treatments and error (Table 36.7).

Demerits:

This design can only be used when the number of treatments to be used forms a square. Moreover, the analysis of variance is complicated.

The ANOVA table of a 5 x 5 lattice with 3 replications is given below:

where, r = number of replication and p = square root of treatments.

Experimental Design: Type # 6. Augmented Designs:

The concept of augmented design was developed by Federer (1956). This is an experimental design which is used to test a large number of germplasm lines in a limited area.

The important characteristics of this design are given below:

i. Layout:

In this design, standard or check varieties are replicated among the cultures. Thus, standards are replicated and cultures are non-replicated. The number of check varieties should be at least 4.

ii. Replications:

The number of replications depends on the number of check varieties to be used. For example, if we have 4 check varieties we should have a minimum of 5 replications to get more than 10 error degrees of freedom.

iii. Randomization:

The check varieties are first randomly allocated to the plots of each block, and the germplasm lines are then randomly allocated to the remaining plots of each block.

Merits:

This is an ideal and efficient design for testing a very large number of germplasm lines at a time with small quantity of seed, on a limited piece of land.

Demerits:

The analysis of augmented design is very much complicated. In this design, the comparison of cultures within a replication is easy but to compare culture of one replication with that of another is very tedious job. In this design, there is no proper check of fertility variation.

The construction of the augmented randomized complete design using 5 blocks, 4 varieties (A, B, C, and D) and 15 germplasm lines (e, f, g, h, i, j, k, l, m, n, o, p, q. r and s) is illustrated below: