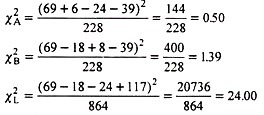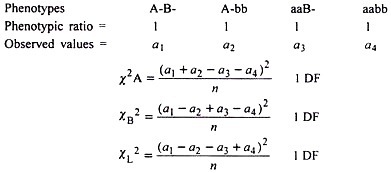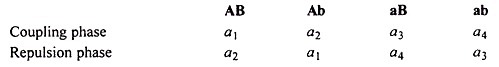Detection of Linkage | Genetics

After reading this article you will learn about:- 1. Detection of Linkage Using F2 Data 2. Detection of Linkage Using Backcross (Testcross) Data.

Detection of Linkage Using F₂ Data:

It may be recalled that when 2 genes are located on 2 different chromosomes, they assort independently and give rise to a typical 9:3:3:1 ratio in the F₂ generation assuming complete dominance at both the loci. Under this situation, typical backcross (testcross) ratio is 1 : 1 : 1: 1. Failure of fulfillment of these ratios is an indication of abnormal segregation at either loci or involvement of linkage.

When an F₂ data fails to conform to a 9 : 3 : 3 : 1 ratio as revealed by χ² test, the χ² is partitioned into various components to confirm if linkage is involved as explained below:

When only 2 classes al and a2 are available in a ratio of 1₁ : 1₂, χ² can be calculated using direct values also using the formula:

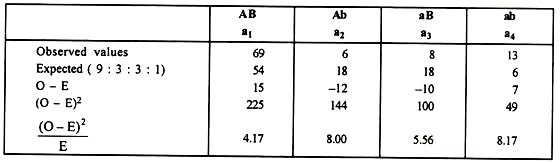
Numerical Illustration:

χ²_T = 4.17 + 8.00 + 5.56 + 8.17 = 25.90

χ²_T with a value of 25.90 is highly significant at 3 degrees of freedom indicating non- fulfillment of 9 : 3 : 3 : 1 ratio.

Hence, this χ² value is partitioned into components as:

Each of above 3 χ² values has 1 degree of freedom. Calculated χ_A² is not significant showing normal segregation at A locus. Similar is the case at B locus. However, χ_L² is significant clearly showing that significant departure from 9: 3: 3: 1 F₂ ratio in the original data can be ascribed to linkage.

Detection of Linkage Using Backcross (Testcross) Data:

Numerical Illustration:

The backcross (testcross) data is tested for goodness of fit for the expected ratio 1:1:1:1. In the event of failure of this hypothesis, the resultant χ² is partitioned as given above, for example:

The data clearly shows that it does not fit to 1: 1: 1: 1 ratio. Further after partitioning of X² (33.84), into X_A², X_B² and X_L², the linkage is apparent.

The formulae as given above for F₂ and backcross data are valid for coupling phase (both the dominant genes in one parent and both the recessive genes in another parent).

The same formulae are applicable to repulsion phase data (AAbb x aaBB) also but the classes are inverted as: