Chi-Square Test and its Interpretation | Genetics

After reading this article you will learn about the chi-square test and its interpretation.

In genetic experiments, certain numerical values are expected based on segregation ratios involved. However, in actual field experiments exact values may not be obtained due to in-viability of certain pollen grains, zygotes, no germination of some seeds, or even death of few plants after germination.

This leads to some deviation between the actual results and the expected ones under a given hypothesis. The chi-square (X²) test is an statistical test to determine whether the deviation is within the limits of experimental error or large enough to reject the hypothesis involved.

The formula of chi-square is symbolized as follows:

Where

O = the observed number;

E = expected number

Σ = Sigma, the summation sign

The value is calculated for the degrees of freedom n-1 where n is the number of classes.

Limitations of X² Test:

(i) It is used only on the numerical data, not on the percentages or ratios.

(ii) It cannot properly be used when expected frequency within any phenotypic class is less than 5.

Correction for Small Sample:

Yates’ correction as given below is applied:

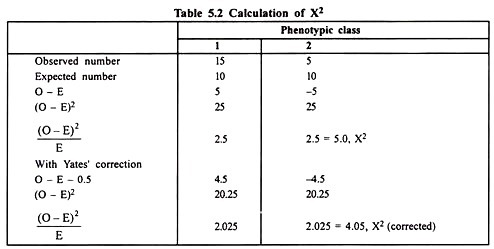
Numerical Illustration:

In an experiment observed values in 2 phenotypic classes are 15 and 5 and expected values based on 1 : 1 ratio (monogenic testcross) will be 10 and 10 respectively.

The X² without and with Yates’ correction is as follows:

Interpretation of X²:

After determination of X² and degrees of freedom, a table (Table 5.3) is consulted to find out the probability of occurrence of chance deviations (between observed and expected values) as large as or larger than those observed. Greater the probability, lesser is the risk in accepting the hypothesis. A hypothesis is never proved or disproved by a probability (P) value.

The 5% point (P = 0.05) is usually chosen as an arbitrary standard to determine the significance or goodness of fit. P = 0.05 means that the deviations as large as observed or larger than observed shall occur only 5 times out of 100 cases on account of chance factor.

Under this kind of situation the hypothesis is rejected. This probability value also means that a true hypothesis will be rejected once in 20 cases. Sometimes P equalling 0.01 is used as level of significance indicating that the probability of rejecting a true hypothesis is still smaller i.e., 1/100 only.

Here also the hypothesis is rejected. For accepting the hypothesis P must be more than 0.05. Another approach to arrive on same conclusions is to compare the calculated value of X² with the table value at P = 0.05 for a given degree of freedom. If the calculated value is less than the table value, the goodness of fit of the given ratios is accepted otherwise rejected.