Regression Analysis and Regression Lines in Statistics

In this article we will discuss about the Regression Analysis and Regression Lines in Statistics.

Meaning of Regression:

Regression means to return or come back. It is used in the cases where the values of data of two or more series tend to return toward the mean of the series. Sir Francis Galton observed that tall fathers produced tall sons and the dwarf fathers produced dwarf sons.

The average height of tall sons was found to be less than the average height of fathers. Similarly, the average height of dwarf sons exceeded the average height of their dwarf fathers. This tendency of height in human beings to move towards the average height was called regression by Galton.

In biological studies it is important to know how the variation in one variable affects the variation in other variable, as for example, the yields of wheat vary with the change in the amounts of fertilizers applied as well as the change of plant density, and similarly, the weights of animals vary with the change of protein contents in feed.

In such problems, it may be possible to distinguish the variable of primary interest and one or more variables of secondary interest which affect the main one. The main variable is called dependent variable which is denoted by Y and the secondary variables are called independent variables which are denoted by X.

Thus, the change in the yield of wheat is dependent variable (Y) and the change in the amounts of fertilizers applied is independent variable (X) which affects the yield potency.

Regression Analysis:

The purpose of regression analysis is to predict the value of one character or variable (say Y) from the known value of the other variable (say The value of variable to be predicted is dependent variable and the known variable is called the independent variable. The regression analysis is done by (i) Regression lines and (ii) Regression coefficient.

Regression lines explain the mean relationship between X and Y variables.

Kinds of Regression Analysis:

In general, there are two types of Regression analysis:

1. Simple Regression:

It involves two variables, one of which is independent and the other dependent. It may be classified into Linear and non-linear or curvilinear regressions.

2. Multiple Regression:

It involves more than two variables. In this, the number of independent variables may be two or more than two.

A linear regression problem is one in which the same change in dependent variable Y can be expected for a change in the independent variable X irrespective of the value of X. In this case, a mathematical function representing a straight line graph can be used to describe the relationship between the two variables.

In other words, the two variables show linear relationship when the change in independent variable X causes a change in dependent variable Y.

For illustrating linear regression, let us consider the following data recorded on 7 animals:

The relationship between dependent variable (weight) and independent variable (age) may be illustrated in the form of scatter diagram by plotting weights (Y) against ages (X) Fig. 35.1.

It is evident from the scatter diagram that there is a linear relationship between weight and age, i.e, weight is affected by age or in statistical terms; there is a linear regression of weight on age. The line passing through the majority of the dots or the line of best fit is referred to as regression line.

If the regression line is straight the regression is said to be linear regression and if the regression line is curved then it is called curvilinear or non-linear regression.

When two variables X and Y are plotted on a scatter diagram, two lines of best fit can be drawn which pass through the plotted points. These lines are called regression lines and two equations based 1-41 these 2 lines are called regression equations.

Regression Lines:

The composition of regression lines is based on the least square assumptions. Regression analysis is generally based on the summation of squares of deviations of observed values of from the lines of the best fit. A line of regression gives the best average value of one variable from any given value of the other variable.

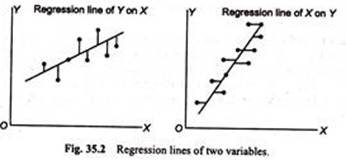
In regression analysis, there are usually two regression lines to show the average relationship between X and Y variables. It means that if there are two variables X and Y, then one line represents regression of Y upon x and the other shows the regression of x upon Y (Fig. 35.2).

On these lines if the value of one variable is known, the corresponding value of variables on the other axis can be obtained. When the regression lines are nearer to each other then there is a high degree of correlation between X and Y.

Another explanation for two regression lines is that regression lines are the lines of best fit which are made on the basis of assumptions of least squares of deviations of observed values. Accordingly, the lines of best fit are those which represent the minimum values of deviation squares of observed values.

Deviations can be measured in two ways:

(i) Horizontally, and

(ii) Vertically.

To get the minimum of two deviations, two lines are essential. That line on which the sum of the squares of horizontal deviations is minimum is called regression line of X and Y the line on which the sum of the squares of vertical deviations becomes minimum is called regression line of Y on X.

If X = 0, both the variables are independent and they will cross each other at right angle. When the regression lines intersect each other at the point of means of X and Y, and if a perpendicular line is drawn from that point to the X axis, it will touch the axis on the mean value of X. Similarly, if another perpendicular line is drawn from that point to the Y axis, it will touch the Y axis at the mean value of y (Fig. 35.3).

The lesser the correlation, the greater will be the divergence of angles. The steepness of the regression lines indicates the extent of correlation. Closer the correlation, the greater is the steepness of regression lines X and Y or Y and X.