Centrifugation: Theory, Sedimentation Rate, Coefficient and Other Details

If a container is filled with a suspension of particles of varying size and density, the particles will gradually settle to the bottom of the container under the influ­ence of gravity.

The rate at which settling occurs can be greatly increased by increasing the gravitational effect on the particles. This is the rationale behind the use of centrifugation.

A tube containing a suspension of particles (e.g., a tissue homogenate) is placed in the rotor of a centrifuge and then is rotated at high speed.

The resulting acceleration greatly increases the force acting on the suspended particles, causing their more rapid sedimentation to the bottom of the tube along paths that are perpendicular to the axis of rotation (i.e., along radii of the circle being swept out by the ro­tating tubes; see Fig. 12-1).

Although the practical application of centrifugal force can be traced back more than a thousand years, the modern era of centrifugal methodology began in the early years of this century when the focal point of biochemistry was the study of the chemical and physi­cal properties of protein solutions and other colloids. The discovery by Emil Fischer in 1902 that proteins consisted of long chains of amino acids turned out to be the main impetus behind a dramatic surge in the development of centrifugal methods.

Fischer and most other notable chemists of the period believed that individual protein species (myoglobin, hemoglo­bin, etc.) were polydisperse; that is, a given protein type was believed to occur in various sizes (i.e., vari­ous polypeptide chain lengths). That this is not the case was shown by Theodor Svedberg, who developed the first “analytical ultracentrifuges” (see below), in which the movements of sedimenting particles can be followed optically.

Svedberg showed that a given pro­tein type is not polydisperse but is homogeneous (or mono-disperse), with all molecules of that protein hav­ing the same, well-defined molecular weight. In 1926, Svedberg received the Nobel Prize in recognition of his pioneering centrifugal studies of proteins and other colloids.

Theory of Centrifugation:

The force acting on a particle during centrifugation is given by the equation:

F = mω²x (12-1)

Where to is the mass of the particle, ω (omega) is the angular velocity of the spinning rotor in radians per second (one unit of circumference contains 2π radi­ans), and x is the distance of the particle from the axis of rotation.

Usually, the value given for the force applied to par­ticles during centrifugation is a relative one; that is, it is compared with the force that the earth’s gravity would have on the same particles. It is called relative centrifugal force or RCF and is given by

Where g is acceleration due to gravity and equals 980 cm/sec/sec.

Because g is a constant, then

In equation 12-3, the term (27r/60)/980 is also a con­stant and is equal to 1.119 x 10^-5.

Thus the equation for relative centrifugal force (i.e., equation 12-2) simplifies to

RCF = 1.119 x 10^-5 (rpm)² (12-4)

Consequently, to determine the relative centrifugal force in effect during centrifugation it is necessary to measure the revolutions per minute (rpm) of the rotor and the distance between the sample and the axis of rotation. Because RCF is the ratio of two forces, it has no units. However, it is customary to follow the nu­merical value of the RCF with the symbol g. This indi­cates that the applied RCF is a multiple of the earth’s gravitational force.

Sample Problem:

What is the maximum relative cen­trifugal force applied when red blood cells are sedimented at 1000 rpm in a rotor of maximum sample ra­dius equal to 10 cm?

RCF_max = 1.119 x 10^-5 (1000)²(10)

= 1.119 x 10² or 112g

The sedimentation of particles by centrifugation is, in effect, a method for concentrating them; therefore, one of the major physical forces opposing such concen­tration is diffusion. In the case of the sedimentation of cells or sub-cellular organelles (nuclei, mitochon­dria, etc.), the effects of diffusion are essentially nil. However, when centrifugation is used to sediment much smaller particles (such as cellular proteins, nu­cleic acids, or polysaccharides), the effects of diffusion become significant.

Sedimentation Rate and Sedimentation Coefficient:

The RCF or “g force” applied to particles during cen­trifugation may readily be calculated using equation 12-4 and is independent of the physical properties of the particles being sedimented. However, a particle’s sedimentation rate at a specified RCF depends on the properties of the particle itself.

Also, because the RCF varies directly with x, it is clear that the sedi­mentation rate changes with changing distance from the axis of rotation. (For particles settling under the influence of the earth’s gravity alone, the sedimenta­tion rate is constant.)

The instantaneous sedimenta­tion rate of a particle during centrifugation is deter­mined by three forces:

(1) F_C, the centrifugal force,

(2) F_B, the buoyant force of the medium, and

(3) F_F, the frictional resistance to the particle’s movement.

Equation 12-13 is very important to the understand­ing of particle sedimentation and should be carefully examined, for the equation shows that those proper­ties of a particle that determine its rate of sedimenta­tion during centrifugation are radius and effective density (i.e., the difference between the density of the particle and the density of the liquid through which the particle is sedimenting).

Because the sedimenta­tion rate varies in proportion to the square of the par­ticle’s radius (but is a first-order function of the parti­cle’s density) it is clear that particle size is “more influential” than particle density in determing sedi­mentation rate.

From equation 12-13, it may also be noted that two particles having different sizes or different densities can have similar sedimentation coefficients. On the other hand, two particles with either similar size or similar density can have markedly different sedimen­tation coefficients.

The Analytical Ultracentrifuge:

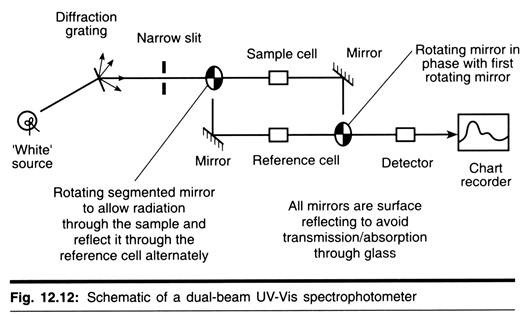
The sedimentation coefficient of a particle may be de­termined experimentally using an instrument known as an analytical ultracentrifuge. The rotor that spins in this ultracentrifuge typically contains two compart­ments. Into one compartment is placed a “reference cell” containing sample-free solvent and the other re­ceives a cell containing the sample to be analyzed. The interior of each cell is sector shaped and bounded above and below by parallel quartz windows to permit light from below the rotor to pass through the refer­ence and sample during rotation (Fig. 12-2).

As the particles sediment, boundaries are formed at the trail­ing edges of each particulate species. Changes in the distance between each boundary and the axis of rota­tion are measured as a function of time by the instru­ment’s optical system.

These measurements are then used to calculate the respective sedimentation coeffi­cients of the particles in the suspension. The sharp­ness of the boundaries that are formed serves as an in­dex of the heterogeneity of the sample. The first analytical ultracentrifuges were de­signed and built by T. Svedberg in the 1920s.

The sedimentation coefficients of many cellular macromolecules such as proteins and nucleic acids fall in the range of 1 x 10^-13 to 200 x 10^-13 seconds (i.e., the dimensions of s are seconds). For convenience, a unit called the Svedberg unit (named in honor of T. Sved­berg), abbreviated S, is used to describe sedimenta­tion coefficients and is equal to the constant 10^-13 sec­onds. Thus, most cellular proteins have sedimentation coefficients between 1 and 200 S. The sedimentation coefficients of a number of cell constituents are listed in Table 12-1.

Calculation of the sedimentation coefficient from data collected with the analytical ultracentrifuge involves the following amplification of the relationship of equation 12-12. If a boundary is x₁ centimeters from the axis of rotation at time t₁ and x₂ centimeters at time t₂, then equation 12-12 may be solved by integration as follows. First, by transposition,

Sample Problem:

A solution containing a single partic­ulate species is accelerated in the analytical ultracentri­fuge at 60,000 rpm. At time t_1; the boundary between the trailing edge of the sedimenting particles and the axis of rotation is 6.0 cm, while at t₂, 60 minutes later, the boundary is 6.8 cm from the axis. What is the sedimenta­tion coefficient of the particles?

As its name implies, the analytical ultracentrifuge is an instrument for analysis and does not physically separate the multiple components of a mixture from one another. Furthermore, the amount of material that may be studied is quite limited as a result of the small size of the rotor’s sample cell.

Preparative Centrifugation:

The counterpart to analytical centrifugation is pre­parative centrifugation, which provides for the isola­tion of cell components for further analysis. Two basic types of centrifuge rotors are regularly employed for conventional preparative centrifugation; these are the swinging-bucket rotor and the fixed-angle rotor (Fig. 12-3).

The swinging-bucket rotor consists of a series of metal buckets attached to the central harness of the rotor. The samples to be centrifuged (previously placed in centrifuge tubes) are inserted into the buck­ets, which swing upward from a vertical position to a horizontal position during acceleration of the rotor (Fig. 12-3).

During deceleration, the buckets return to the vertical position and the centrifuge tubes are then removed. In a fixed-angle rotor, the centrifuge tubes are maintained at a constant angle (usually 15° to 45° from verticality) throughout centrifugation (Fig. 12-3). As a result, the radially sedimenting par­ticles quickly strike the tube wall, where convection currents help to carry them to the bottom of the tube.

Differential Centrifugation:

During centrifugation, particles sediment through the medium in which they are suspended at rates related to their size, shape, and density. Differences in the sedimentation coefficients of the various subcellular particles provide the means for their effective separa­tion.

Differential centrifugation, a technique intro­duced to cellular research in the early 1940s by the noted biologist and Nobel laureate Albert Claude, is one of the classic procedures for isolating subcellular particles and involves the stepwise removal of classes of particles by successive centrifugations at increas­ing RCF.

The material to be fractionated is subjected first to low-speed centrifugation to sediment the largest (or densest) particles present. Following this, the unsedimented material (called the supernatant) is trans­ferred to another tube and centrifuged at a higher speed (and usually also for a longer period of time) to sediment particles of somewhat smaller size (and/or lower density).

The sequence is repeated several times until all particles have been sedimented; each sediment is then used for further experimentation and analysis. The procedure that is routinely used for the differential fractionation of liver tissue serves as a convenient example of this method and is shown diagrammatically in Figure 12-4.

The removed liver tissue is homogenized in cold buffer and centrifuged 10 minutes at 700 g. This is usually sufficient to sediment all the cell nuclei to the bottom of the centrifuge tube, thereby providing the nuclear fraction. Depending on the effectiveness of the homogenization procedure, some unbroken cells and large cell fragments may also be recovered in this fraction.

The overlying supernatant (called the nu­clear supernatant) is removed and transferred to an­other tube for a second centrifugation at 20,000 g for 15 minutes. These sediments nearly all the mitochon­dria (i.e., the mitochondrial fraction).

Again, the su­pernatant (i.e., mitochondrial supernatant) is re­moved and is subjected to a third centrifugation at 105,000 g for 60 minutes. This causes the sedimenta­tion of a fraction called microsomes, which includes ribosomes and small fragments of intracellular mem­branes.

The microsomal supernatant is referred to as the soluble phase of the cells, or cytosol, and includes soluble proteins, soluble nucleic acids, soluble polysac­charides, lipid droplets, and other minute particles. In the procedure just described the liver tissue is sepa­rated into four major fractions.

Markers:

The most widely used methods for identi­fying the constituents of fractions produced by centrifugation involve microscopy and chemical and bioassays for specific markers. Although the light mi­croscope may be used to successfully identify the larger cellular structures such as nuclei, chloroplasts, and mitochondria, the identification of smaller parti­cles such as peroxisomes and ribosomes requires electron microscopy.

Certain enzymes and other mole­cules may be peculiarly associated with a particular cell component and therefore readily serve as mark­ers. For example, the enzyme succinic dehydrogenase is found exclusively in mitochondria; consequently, any centrifugal fraction that exhibits succinic dehy­drogenase activity would be expected to contain mito­chondria.

Chloroplast-rich fractions exhibit ribulose diphosphatase activity, plasma membrane-rich frac­tions exhibit adenylate cyclase activity, and so on. Ta­ble 12-2 lists some of the more useful and reliable markers used in the identification of the components present in the tissue and cell fractions produced dur­ing centrifugation. It should be noted that not all markers are enzymes; DNA is an excellent marker of nuclei-rich fractions and chlorophyll is an excellent chloroplast marker.

Differential centrifugation has several major disad­vantages. Because the homogenate is initially distrib­uted uniformly throughout the centrifuge tube, the first particles sedimented will necessarily be contami­nated with small amounts of all other constituents of the homogenate. This effect is shown in Figure 12-5.

As the smaller particles are sedimented, they in turn will be contaminated by even smaller particles. In fact, the only particles obtained in relatively pure form will be those that sediment most slowly. In the example given above, the initial nuclear fraction would contain some mitochondria, microsomes, and cytosol; the mitochondrial fraction obtained in the second cen­trifugation would be contaminated with microsomes and cytosol, and so on.

These disadvantages may not be serious in some instances, because the major sub­cellular particles of a tissue homogenate have sedi­mentation coefficients that differ from one another by one or more orders of magnitude. However, serious difficulties arise if the particles to be separated have similar sedimentation coefficients. This problem is il­lustrated in Figure 12-4f, in which the mitochondrial fraction also contains the cells’ lysosomes.

Density Gradient Centrifugation:

The resolution achieved during centrifugation can be greatly improved if the mixture of particles is con­fined at the outset to a narrow zone at the top of the centrifuge tube and the particles then permitted to sediment from this position.

Initial stability under these conditions can be obtained only if the particles are layered onto a density gradient, that is, a column of fluid of increasing density. This technique, known as density gradient centrifugation, was introduced to cellular research in the late 1940s and early 1950s by N. G. Anderson and M. K. Brakke and is an exceed­ingly powerful preparative tool.

Density gradients may be stepwise (discontinu­ous) or continuous. A step gradient is prepared by successively layering solutions of decreasing density in the centrifuge tube. Continuous density gradients are prepared by mixing dense and light solutions in varying proportions at a controlled rate and delivering the mixture to a centrifuge tube in a continuous stream.

A simple procedure for producing a “linear” density gradient is shown in Figure 12-6. In this pro­cedure, the light solution (in the right cylinder) flows into and is mixed with the dense solution (in the left cylinder).

The mixture is then delivered to the centri­fuge tube. Using this method, a density gradient is formed that decreases linearly as a function of volume between the limiting densities originally present in the two cylinders.

Gradients with other shapes (expo­nential, hyperbolic, etc.) may be prepared using con­tainers of various non-cylindrical shapes or gradient- generating devices specifically manufactured for this purpose. Solutes used to provide solutions for density gradients are selected on the basis of their solubility in water and their compatibility with cells and subcellu­lar organelles.

Sucrose, Ficoll (a copolymer of sucrose and epicholorhydrin), Metrizamide, Nycodenz, and Percoll (a colloidal form of silica) are the most popular, as they have minimal detrimental effects on organelles and provide densities up to about 1.3 g/cm Ce­sium chloride, cesium trifluoroacetate, and other dense salts are used when the limiting density must be considerably higher (i.e., up to 1.9 g/cm). The rate at which particles sediment through a density gradi­ent is given by equation 12-13. Because the quantity (ρ_P – ρ_M) changes as the particles sediment deeper into the gradient, s also changes.

If a particle reaches a po­sition in the gradient where the particle’s density and the gradient’s density are the same (i.e., ρ_P = ρ_M), then s becomes zero, and no further sedimentation of the particle occurs. If a particle suspension is overlaid with a gradient whose maximum density is greater than that of the particles (i.e., ρ_M > ρ_P), then during centrifugation the particles will rise through the gra­dient, for when ρ_M is greater than ρ_P, s becomes a neg­ative term.

Rate Sedimentation:

When the densest region of a density gradient (i.e., the liquid at the bottom of the centrifuge tube) is less dense than the particles being sedimented, all particles will eventually reach the bot­tom of the tube (if centrifugation is continued long enough).

However, if the duration of centrifugation is carefully limited, this will not occur; instead, the par­ticles will be distributed through the density gradient in the order of their sedimentation coefficient. Frac­tionations carried out in this manner are called rate separations and are based on the combined contribu­tions of particle size and particle density. The rate fractionation of a liver tissue homogenate is depicted in Figure 12-7. The four major cell fractions (nuclear, mitochondrial, microsomal, and cytosol) are separated during a single centrifugation.

Isopycnic Sedimentation:

When the densest region of a density gradient is denser than any of the parti­cles to be sedimented, none can reach the bottom of the tube regardless of how long centrifugation is carried out. Instead, the particles will sediment through the gradient until they reach their isodense or isopycnic position.

Fractionations carried out on the basis of particle density alone are called isopycnic separations. It is to be noted that this implies that small, dense particles with low sedimentation coefficients sediment further through such a density gradient than large, light particles with high sedimentation co­efficients (Fig. 12-8).

In rate separations, both particle size and particle density determine the final positions of particles in the gradient. However, of the two parameters, size is more influential because s is a second-order function of particle radius but a first-order function of particle density. In isopycnic sepa­rations, particle density alone determines final posi­tion in the density gradient. Figure 12-9 compares the sedimentation coefficients and densities of a vari­ety of cellular components.

In certain instances, it is not necessary to layer the sample to be fractionated onto a preformed density gradient. Instead, the sample and the density gradi­ent solutions are mixed and placed in the centrifuge tube. During centrifugation at high speed, the density gradient forms automatically within the tube, and particles migrate (upward and/or downward) to their isopycnic positions. This procedure is known as equi­librium isopycnic centrifugation and is regularly carried out using solutions of CsCl or other heavy salts (Fig. 12-10).

Although density gradient centrifugation is usually carried out in swinging-bucket rotors, isopycnic (but not rate) separations can also be performed in fixed- angle rotors (Fig. 12-11a). When the gradient with sample layered above is placed in the inclined position in the rotor, the sample zone and equal density planes within the gradient form ellipses.

During acceleration of the rotor, each isodense elliptical layer becomes a small section of a paraboloid of revolution with focal point on the axis of rotation. The family of paraboloids becomes increasingly steep as rotor acceleration con­tinues and eventually approaches vertically; this phe­nomenon is called gradient reorientation.

Particles in the gradient sediment radially until they encounter the sloping tube wall; from there, they are carried down through the gradient by centrifugal force and convection until they reach the isodense region of the gradient, where they form layers. Rotor deceleration reorients the gradient again so that the separated par­ticles form horizontal layers.

A recent modification of the fixed-angle approach to isopycnic centrifugation involves the use of vertical tube rotors in which the fixed angle is reduced to 0 (i.e., the centrifuge tubes are maintained in the verti­cal position throughout; Fig. 12-11b). Here, too, the gradient is reoriented during rotor acceleration and deceleration.